Soil Heat Flow and Continuity Equation
ABSTRACT
Soil thermal parameters are mainly inputs for models of soil heat flux. Mathematical models are important tool for predicting the soil heat and water transfer, depending on some fundamentals of soil physical properties. Soil moisture is one of the soil physical properties that have a great effect on thermal parameters. The aim of the work is to describe the behavior of soil thermal parameters under different values of soil moisture, and is to investigate the effect of some fundamentals of soil physical properties on thermal parameters. We could describe the relationship between thermal diffusivity and soil moisture by ∩ shaped curve using a quadratic equation and evaluate the efficiency of this equation, statistically. Experimental thermal diffusivity (Kexp) by direct method and mathematical models were measured. Mathematical models were Chung and Horton model (1987) (Kcal-2), the model of Arkhangel'skaya (2004) (Kcal-3) and the suggested quadratic equation (Kcal-1). Efficiency of the quadratic equation and mathematical models were estimated using the correlation coefficient (R2), Root Mean Square Error (RMSE), and the Nash-Sutcliffe Efficiency (NSE). The values of R2, RMSR and NSE for the quadratic equation were 0.978, 0.24 and 0.95, respectively, for sod-podzolic soil under the study. The quadratic equation is a simple and faster equation for forecasting soil thermal diffusivity.
Key words: Soil thermal parameters, thermal diffusivity, thermal conductivity, soil heat capacity, soil moisture, soil bulk density, organic matter, quadratic equation and mathematical models.
INTRODUCTION
Soil thermal parameters are playing an important role in many, chemical, biological, physical and environmental processes such as the dew, soil aeration, crop growth (Timlin et al., 2002), soil CO2 production (Buchner et al., 2008; Bauer et al., 2012), ecosystem carbon sequestration (Ju et al., 2006), and subsurface soil water evaporation (Sakai et al., 2011). Usually, the soil heat transport simulations are based on estimates of the soil thermal conductivity and soil thermal diffusivity as a function of the soil water content. Moreover, (Votrubova et al., 2012) noted that the simulated soil thermal conditions are strongly affected by the root water uptake approximation. Several authors have suggested models to estimate soil thermal parameters as a function of soil moisture: (Chung and Horton, 1987) estimated the thermal conductivity as a function of soil moisture; also (Evett et al., 2012) described the thermal conductivity as a function of soil moisture and soil bulk density. On the other hand, (Tikhonravova and Khitrov, 2003) suggested a polynomial equation to estimate soil thermal diffusivity as a function of soil moisture as:
K=K0+a1ðœƒ+a2ðœƒ2+a3ðœƒ5
where K0, a1, a2 and a3 are the parameters of the equation. Moreover, (Arkhangel'skaya, 2004) proposed another kind of equation a lognormal equation dependence on thermal diffusivity from water content. (Arkhangel'skaya et al., 2015) described the relationship between thermal diffusivity and water content by S- shaped curve. The vertical one dimensional flux density of heat (JH (W m-2)) in soil is given by Fourier's la,
.png)
where λ is soil thermal conductivity (J m-1 s-1 oC-1), T is temperature in oC and z is soil depth.
λ could be considered as the apparent soil thermal conductivity, as latent heat transfer cannot be separated from conduction in moist soils.
λ = λ *+Dvapor L
λ* is the instantaneous thermal conductivity, D is the thermal vapor diffusivity; L is the latent heat of vaporization (2.449 MJ/kg or 585 cal/g).
Combining the heat flux equation with the equation for conservation of heat energy results in a general expression for soil heat flow, where soil temperature may vary in time and space. The continuity equation of heat in the soil refers that the variation of temperature in time is the result of the additions and losses of energy. This equation is suggested by (Carlslaw and Jaeger, 1964; Nerpin and Chudnovsky, 1975; Kondo and Saigusa, 1994).
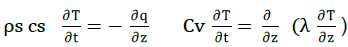
The theoretical investigation (Shein and Karpachevskyi, 2007) indicates that the variation of temperature in time is the result of the thermal diffusivity, K (cm2/sec), and the changes of temperature through depth (Z cm) by classical equation:
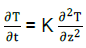
The thermal diffusivity K is the ratio between the thermal conductivity λ (J m-1 sec-1°C-1) and the volumetric heat capacity Cv,  .Where Cv (J g−1 °C−1) is the volumetric heat capacity
.Where Cv (J g−1 °C−1) is the volumetric heat capacity 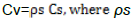 is the apparent density of the soil (Mg/m3), and Cs is the specific heat of the soil. If the soil is homogeneous, then the soil's volumetric heat capacity Cv and thermal conductivity λ are constant with depth. The objective of the current work is therefore to describe the relationships between thermal parameters and some fundamentals of soil physical properties. A second objective was to evaluate the efficiency of suggested quadratic equation. To achieve this objective, the thermal diffusivity was measured by direct method under different soil moisture content levels, then the results were compared with those estimated by mathematical models, so that we could determine which is the best model could be used to forecast thermal diffusivity.
is the apparent density of the soil (Mg/m3), and Cs is the specific heat of the soil. If the soil is homogeneous, then the soil's volumetric heat capacity Cv and thermal conductivity λ are constant with depth. The objective of the current work is therefore to describe the relationships between thermal parameters and some fundamentals of soil physical properties. A second objective was to evaluate the efficiency of suggested quadratic equation. To achieve this objective, the thermal diffusivity was measured by direct method under different soil moisture content levels, then the results were compared with those estimated by mathematical models, so that we could determine which is the best model could be used to forecast thermal diffusivity.
MATERIALS AND METHODS
This study was carried out on sod-podzolic soils of the Moscow region, Zelenograd field laboratory of Soil Science Institute named by V.V.Dokuchaev. Disturbed and undisturbed soil samples were collected from profile layers according to their difference in morphological features. Undisturbed soil samples were taken by metallic cylinders of 5 cm high and 5 cm inner diameter. Particle Size Distribution was estimated using Laser Diffraction method by Analysette-22 according to (Eshel et al., 2004). Organic matter was measured using Express analyser AN-7529. Soil bulk density (ρb) was determined by core method according to (Klute and Dirksen, 1986). Soil particle density (ρs) was determined by pycnometer according to (Blake and Hartge, 1986). Total porosity (n) was calculated using the obtained values of particle and bulk density according to (Klute and Dirksen, 1986).
Experimental thermal diffusivity ( Kexp)
One method for measuring thermal diffusivity K directly in the laboratory is based on placing a heat source, having a constant temperature in contact with the surface of a soil column having constant cross-sectional area and insulated sides. Soil thermal diffusivity (Kexp) was measured in the laboratory by the direct method using Kondratieff method at different values of soil moisture according to (Shein and Karpachevsky, 2007). The levels of soil moisture ðœƒv were 0.02, 0.1, 0.2, 0.35, 0.4, 0.5, and 0.55, cm3/cm3.
Mathematical models
Three models Chung and Horton model (1987) (Kcal-2), the model of Arkhangel'skaya (2004) (Kcal-3), and the proposed quadratic equation (Kcal-1) were used to estimate thermal diffusivity as shown in Table 1. The parameters of Chung and Horton model (1987) b1, b2, and b3 were estimated by fitting the curve, and calculating the thermal diffusivity by indirect method through calculating volumetric heat capacity. They calculated the thermal conductivity using the equation:
λ0 (ðœƒ) =b1+b2ðœƒ+b3𜃠0.5
Where, b1, b2, and b3 are empirical parameters. Volumetric heat capacity Cv was determined by using the formula:
Cv =1.94 (1- n-ɸ) +4.189𜃠v+2.5 ɸ (M J m-3oC-1)
Where: Cv is soil heat capacity, n is the soil porosity; ɸ is the volume fraction of soil organic matter and θ v is the volumetric water content. 2) The parameters of model Arkhangel'skaya (2004), K0, a, w0, and b were determined from curve fitting of thermal diffusivity and soil moisture.
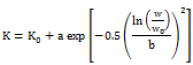
where W is water content, K is the corresponding thermal diffusivity; K0, a, w0, and b are parameters of the curve. K0 is thermal diffusivity of dry soil, w0 is the water content corresponding to the maximum thermal diffusivity. 3) The new suggest quadratic interpolation equation was to estimate thermal diffusivity K (ðœƒ) as a function of soil moisture.
K (ðœƒ) = b1+b2ðœƒ-b3ðœƒ2
The parameters of equation b1, b2 and b3 are b3 were estimated by fitting the curve.

Statistical analysis
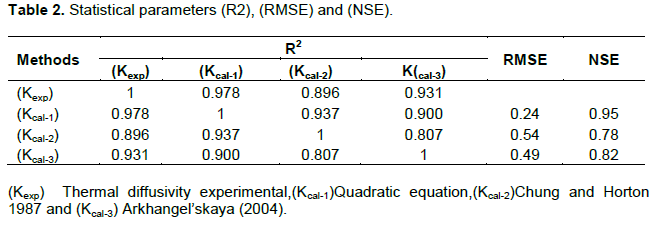
Efficiency of the quadratic equation and mathematical models were determined using the correlation coefficient (R2), Root Mean Square Error (RMSE), and the Nash-Sutcliffe Efficiency (NSE) according to Nash and Sutcliffe (1970).

where Ym is the measured value of K, Yc is the corresponding calculated value of K and Yavg when referring to average of the measured values of K. Modeling efficiencies (NSE) range is from (−∞ to 1), where NSE = 1 corresponds to a perfect match between calculated values and measured data and, NSE = 0 indicates that the model predictions are as accurate as the mean of the measured data, whereas an efficiency <0 (−∞ < NSE < 0) occurs when the model simulations are worse than the measured mean. Software tools were Microsoft Excel, MATLAB, and SPSS program for the Statistical analysis.
RESULTS AND DISCUSSION
Effect of soil moisture on thermal parameters
Effect of soil moisture on thermal diffusivity
Figure 1, shows that thermal diffusivity at first increased rapidly with increasing water content to reach the maximum, then decreased at a slower rate. The maximum value of (Kexp) was 9(cm2/h) at 𜃠v=0.4 cm3/cm3, while the minimum value of (Kexp) was 4.37(cm2/h) at 𜃠v=0.02cm3/cm3. This result agreed with (Arkhangel'skaya et al., 2015) who found out that the maximum thermal diffusivity is observed at a water content of 0.3 to 0.4 cm3/cm3. The reason water content increase thermal contact between soil particles and replaces the air, is that it has lower thermal conductivity than water and increases the specific heat between soil partials. But the thermal diffusivity increases more rapidly than the volumetric heat capacity, as a result, there is a decrease in thermal diffusivity. We could describe the represented data in Figure 1 by ∩ shaped curve using a quadratic interpolation equation.
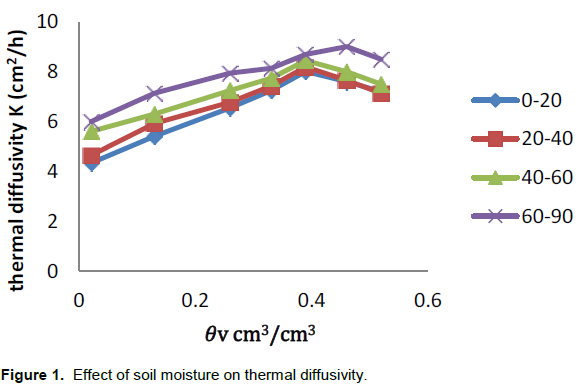
K (ðœƒ) =b1+b2ðœƒ-b3ðœƒ2
where b1, b2 and b3 are the experimental approximated parameters that have an effect on thermal diffusivity; 𜃠is a fraction of volume soil moisture. This description differs from (Arkhangel'skaya, 2004; Arkhangel'skaya et al., 2015) that described the relationship between thermal diffusivity and water content by S - shaped curves with a long gently sloped segment in the region of volumetric water content below 0.15 cm3/cm3, and the region of pronounced increase of thermal diffusivity in the water content has the range from 0.15 to 0.30 to 0.35 cm3/cm3.
Effect of soil moisture on thermal conductivity and heat capacity
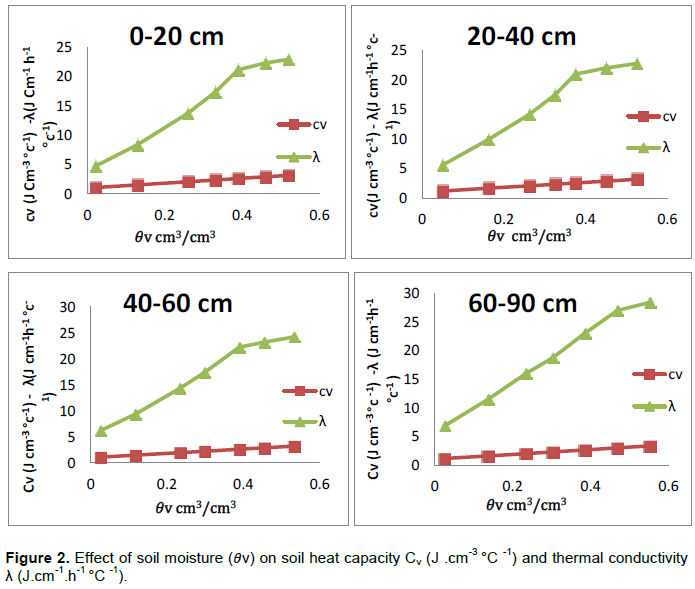
Figure 2 introduces the relationship between soil moisture and each of thermal conductivity and soil heat capacity. The minimum value of λ=4.76 (J cm-1h-1 0Ñ-1) was at 𜃠v=0.02 cm3/cm3 at soil depth (0-20) cm, while the maximum value of λ= 28.50 (J cm-1h-1 0Ñ-1) was at 𜃠v=0.55 cm3/cm3 at soil depth (60 to 90) cm .The thermal conductivity and soil heat capacity increase by increasing soil moisture. Soil heat capacity CV increases linearly with water content, thermal conductivity λ increases more rapidly than Cv at low water contents. This result agreed with (Evett et al., 2012; Oladunjoye and Sanuade, 2012), they found that thermal conductivity and soil heat capacity is based on and increased with increasing soil moisture.
Relationship between thermal parameters and organic matter under different values of soil moisture
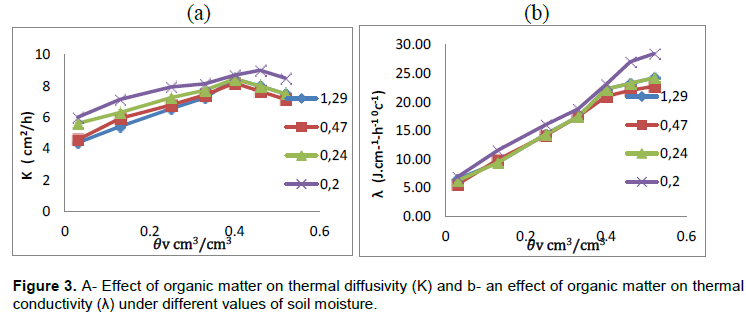
Figure 3, shows that the highest values of thermal diffusivity and thermal conductivity were at the lowest value of organic matter 0.2%, while the lowest values of thermal diffusivity and thermal conductivity were at the highest value of organic matter 1.29%. The reason of that organic matter leads to increase macro pores and soil porosity, due to decreasing contact points between soil particles sequence decrease, thermal diffusivity and thermal conductivity, this result agreed with (Oladunjoye and Sanuade, 2012). There were insignificant negative correlations between organic matter and each of thermal diffusivity and thermal conductivity, were -0.831 and -0.914, respectively.
Relationship between thermal parameters and soil bulk density under different values of soil water content
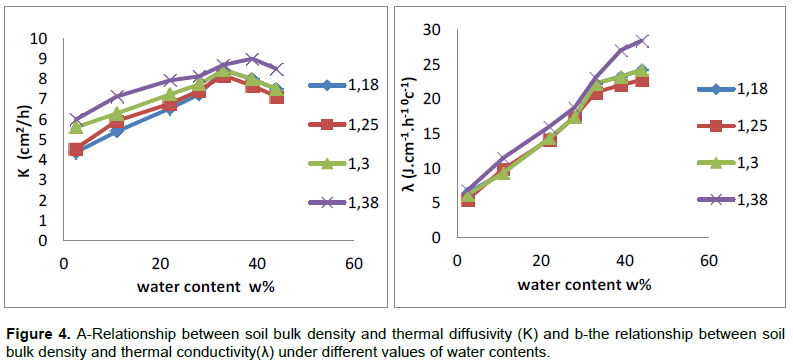
Figure 4 shows that the highest values of thermal diffusivity and thermal conductivity were at the highest value of soil bulk density 1.38 Mg/m3, while the lowest values of thermal diffusivity and thermal conductivity were at the lowest value of soil bulk density 1.18 Mg/m3.The reason of that with depth, increase soil bulk density, where soil particles are better conductors of heat than water, leads to increase conduction of heat between soil particles and increasing thermal parameters, this result agreed with Arkhangel'skaya et al (2015) and Oladunjoye and Sanuade (2012).
Efficiency of the models
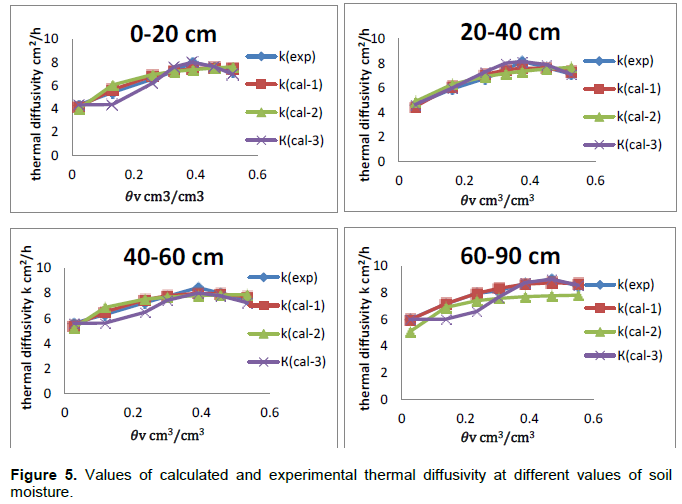
Table 2 shows that the calculated values of K obtained from three models were compared to the corresponding measured value of (Kexp) by direct method. The results observed that the best model could be used to estimate soil thermal diffusivity as a function of soil moisture which was the quadratic equation (Kcal-1), then Arkhangel'skaya model (Kcal-3) and the model of Chung and Horton (Kcal-2), for sod-podzolic soil under the study. (Kcal-1) had the highest values of R2 which was 0.978 and NSE was 0.95, but had the lowest value of RMSE was 0.24. While R2of (Kcal-3) was 0.931, NSE was 0.82 and RMSE was 0.49. On the other hand (Kcal-2) had the lowest values of R2 and NSE, which were 0.896 and 0.78, respectively. While the highest value of RMSE was 0.54. Moreover, Figure 5 shows that the quadratic equation was the best description for the graphical representation of the experiment data, for sod-podzolic soil under the study. The model of Arkhangel'skaya (2004) and Arkhangel'skaya et al. (2015) described the relationship between thermal diffusivity and water content by S -shaped curve. But this description differs from ours as we described thermal diffusivity by ∩ shaped curve that described represented data from experimental thermal diffusivity. While the model of Chung and Horton (1987) was the less efficiency because of it estimated thermal diffusivity by indirect method, through estimated thermal conductivity as a function of soil moisture.
CONCLUSION
Soil physical properties are soil moisture, soil bulk density, particle size distribution and organic matter, which have a great effect on thermal parameters. Thermal diffusivity at first, increased rapidly with increasing water content then decreased at a slower rate. All thermal parameters increased with increasing clay content and soil bulk density (soil depth), while decreased with increasing organic matter and soil porosity. We could describe the relationship between thermal diffusivity and soil moisture by ∩ shaped curve using a quadratic equation. The quadratic equation (Kcal-1) was more efficient than the model of (Arkhangel'skaya, 2004) (Kcal-3) and model of (Chung and Horton, 1987) (Kca-2), for calculating thermal diffusivity as a function of soil moisture. The quadratic equation is a simple and faster equation for forecasting soil thermal diffusivity, for sod-podzolic soil under study. However, it requires more experiments in variant types of soils.
CONFLICT OF INTERESTS
The authors have not declared any conflict of interests.
REFERENCES
| Arkhangel'skaya TA (2004). A New Empirical Formula to Estimate the Thermal Diffusivity of Soil in Proceedings of the Scientific Session on Basic Soil Science, Moscow, Russia. pp. 45-46. | |
| Arkhangel'skaya TA, Luk'yashchenko KI, Tikhonravova PI (2015). Thermal Diffusivity of Typical Chernozems in the Kamennaya Steppe Reserve. Eurasian Soil Sci. 48(2):177-182. | |
| Bauer J, Weihermüller L, Huisman JA, Herbst M, Graf A, Séquaris JM, Vereecken H (2012). Inverse determination of heterotrophic soil respiration response to temperature and water content under field conditions. Biogeochemistry 108:119-134. | |
| Blake GR, Hartage KH (1986). Particle density: Field methods. pp. 377-382. In: A. Klute (ed.). Methods of Soil Analysis. Part 1.2nd ed. Agrnomy Monogr.9. ASA and SSSA, Madiscon,WI. | |
| Buchner JS, Šimůnek J, Lee J, Rolston DE, Hopmans JW, King AP, Six J (2008). Evaluation of CO2 fluxes from an agricultural field using a process-based numerical model. J. Hydrol. 361:31-143. | |
| Carslaw G, Jaeger D (1964). The thermal conductivity of solids. Nauka, Moscow. | |
| Chung SO and Horton R (1987). Soil heat and water flow with a partial surface mulch. Water Resour. Res. 23:2175-2186. | |
| Eshel GGJ, Levy U, Mingelgrin MJ (2004). Singer Critical Evaluation of the Use of Laser Diffraction for Particle-Size Distribution Analysis // Soil Sci. Soc. Am. J. 68:736-743. | |
| Evett SR, Agam N, Kustas WP, Colaizzi PD, Schwartz RC (2012). Soil profile method for soil thermal diffusivity, conductivity and heat flux: Comparison to soil heat flux plates. Adv. Water Resour. 50:41-54. | |
| Ju WM, Chen JM, Black TA, Barr AG, Liu J, Chen BZ (2006). Modeling multi-year coupled carbon and water fluxes in a boreal aspen forest. Agric. For. Meteorol. 140:136-151. | |
| Klute A, Dirksen C. (1986). Hydraulic conductivity of saturated soils. In: Klute, A. (Ed.), Methods of Soil Analysis. ASA & SSSA, Madison, Wisconsin, USA. pp. 694-700. | |
| Kondo J, Saigusa N (1994). Modeling the evaporation from bare soil with a formula for vaporization in the soil pores. Meteorol. Soc. Jpn. 72:413-420. | |
| Nash J, Sutcliffe J (1970). River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 10:282-290. | |
| Nerpin SV, Chudnovsky AF (1975). Energy and mass transfer in the system of plant-soil-air interface. Gidrometeoizdat, Leningrad. | |
| Oladunjoye MA, Sanuade OA (2012). Thermal Diffusivity, Thermal Effusivity and Specific Heat of Soils in Olorunsogo Powerplant, Southwestern Nigeria. IJRRAS 13(2):502-521. | |
| Shein EV, Karpachevskyi LO (2007). Theory and Methods of Soil Physics, (Eds.) Izd. Grif i K, Moscow. | |
| Sakai M, Jones SB, Tuller M (2011). Numerical evalu¬ation of subsurface soil water evaporation derived from sensible heat balance. Water Resour. Res. 47: W02547. | |
| Tikhonravova PI, Khitrov NB (2003). Estimation of thermal conductivity in Vertisols of the Central Ciscaucasus region. Eurasian Soil Sci. 36(3):313-322. | |
| Timlin DJ, Pachepsky Y, Acock BA, Šimůnek J, Flerchinger G, Whisler FD (2002). Error analysis of soil temperature simulations using measured and es¬timated hourly weather data with 2DSOIL. Agric. Syst. 72:215-239. | |
| Votrubova J, Dohnal M, Vogel T, Tesar M (2012). On Parameterization of Heat Conduction in Coupled Soil Water and Heat Flow Modeling. Soil Water Res. 7(4):125-137. | |
doylehasheivates38.blogspot.com
Source: https://academicjournals.org/journal/JSSEM/article-full-text/3330F0260663
0 Response to "Soil Heat Flow and Continuity Equation"
Post a Comment